

CN 11-1911/B


Acta Psychologica Sinica ›› 2020, Vol. 52 ›› Issue (11): 1278-1287.doi: 10.3724/SP.J.1041.2020.01278
• Reports of Empirical Studies • Previous Articles Next Articles
YIN Bin, WU Xiaorui, LIAN Rong( )
)
Received:2020-05-05
Published:2020-11-25
Online:2020-10-10
Contact:
LIAN Rong
E-mail:lianrong1122@126.com
Supported by:YIN Bin, WU Xiaorui, LIAN Rong. (2020). An animal behavioral model for the concept of “Integrative Learning”. Acta Psychologica Sinica, 52(11), 1278-1287.

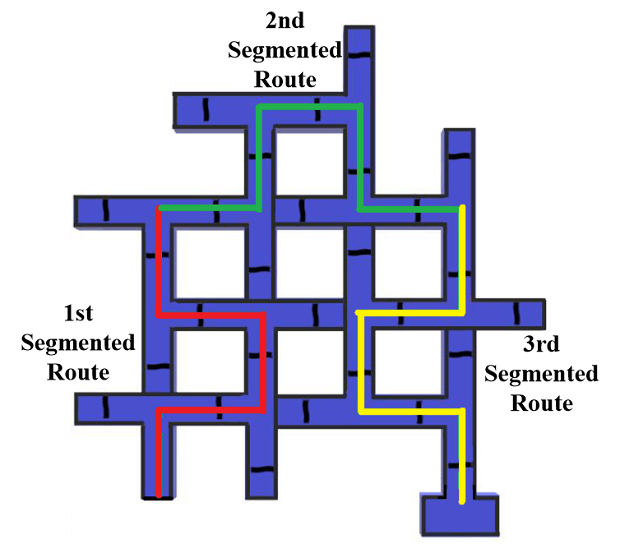
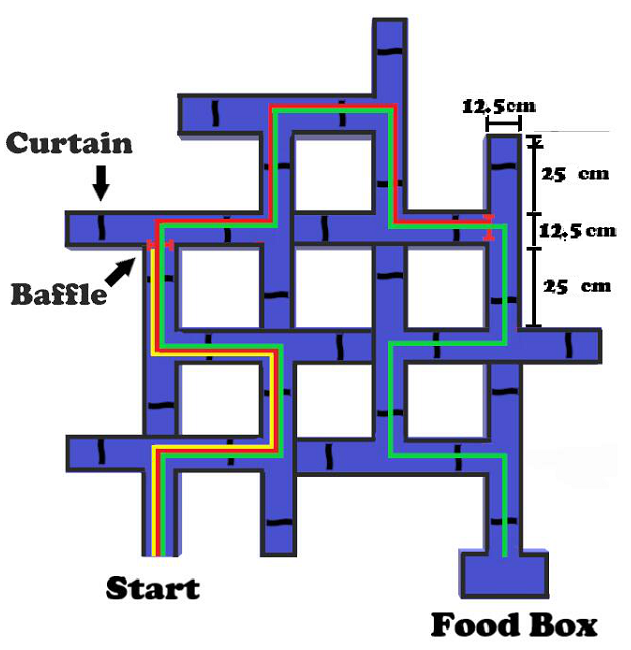
Figure 1. Experimental task design. Note. a) Basic experimental apparatus, modified from Tolman (1948). b) The correct route of the basic experimental apparatus was divided into three segments with shape similarity, and labeled Routes ①, ②, and ③, respectively, in order to facilitate the description of the behavioral characteristics of rats when reporting the results. c) Design of the learning and retesting tasks. The correct route for the PL group was divided into three segments according to the length and regularity of the maze (using a retractable baffle), while the same route for the IL group was not. Here, Route ① (first segment only), Route ② (first and second segments) and Route ③ (all segments) were the correct route for the PL group across Session 1 ~ 3, Session 4 ~ 7 and Session 8 ~ 12, respectively, while Route ③ (all segments) was also the correct route for the IL group across Session 1 ~ 12. During retesting, all segments was kept open. d) Design of the Gestalt (reverse) transfer learning task. The food box entrance was sealed by a partition board and then became the new start area. The curtain of the original starting point was moved to the nearest diverging point to the new start area. e) Design of the generalization/analysis task. Here, Routes ①, ②, and③ were the shortest route, the hidden route and the original route, respectively. f) Design of the segment fixation task. Here, Routes ①, ②, and ③ were the shortest alternative of the first segmented route, the second segmented route and the third segmented route, respectively, and the original route remains unblocked.
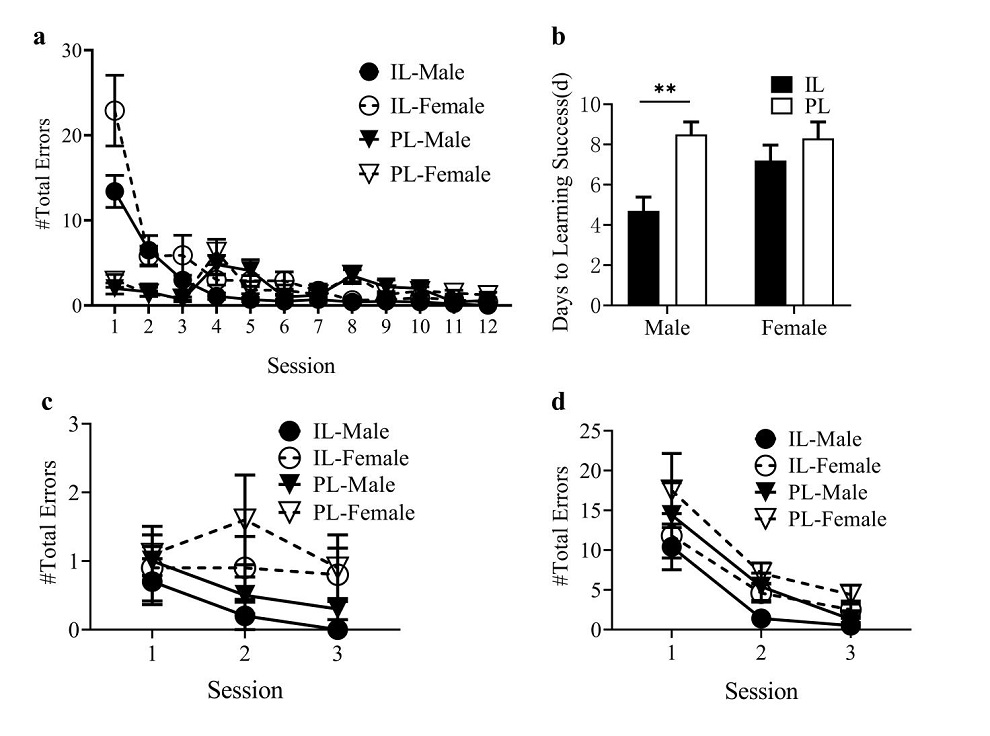
Figure 3. Comparison of learning and memory effects. Note. a) Learning curve: summary of the number of errors during the learning stage. Among them, “#Total Errors” = “#Entry Errors” + “#Detection Errors”, calculated from the beginning of the exploration to the end of the maze. Entry errors refers to the number of times the rat’s head and center entered the wrong area (usually through the curtain), while detection errors refers to the number of times the rat’s head entered the wrong area (however it did not go through the curtain). b) The number of days to learning success. Learning success is defined as the number of days from the first learning session to when it can reliably achieve zero errors when exploring the “open segmented route”. Among them, the “open segmented route” of the IL group is the whole correct route of the maze, so the number of the days before it can reliably achieve zero errors is recorded as the number of days to learning success; however, the “open segmented route” of the PL group is gradually opened in three stages, so the sum of the number of days before it can reliably achieve zero errors in each stage is recorded as the number of days to learning success. c) A chart showing the number of total errors during the retest stage one week after learning. d) A chart showing the number of total errors during the Gestalt transfer learning stage. The position of the circle, triangle or column in each chart shows the average value of each group in each task, and the error bar shows the standard error. **p < 0.01.
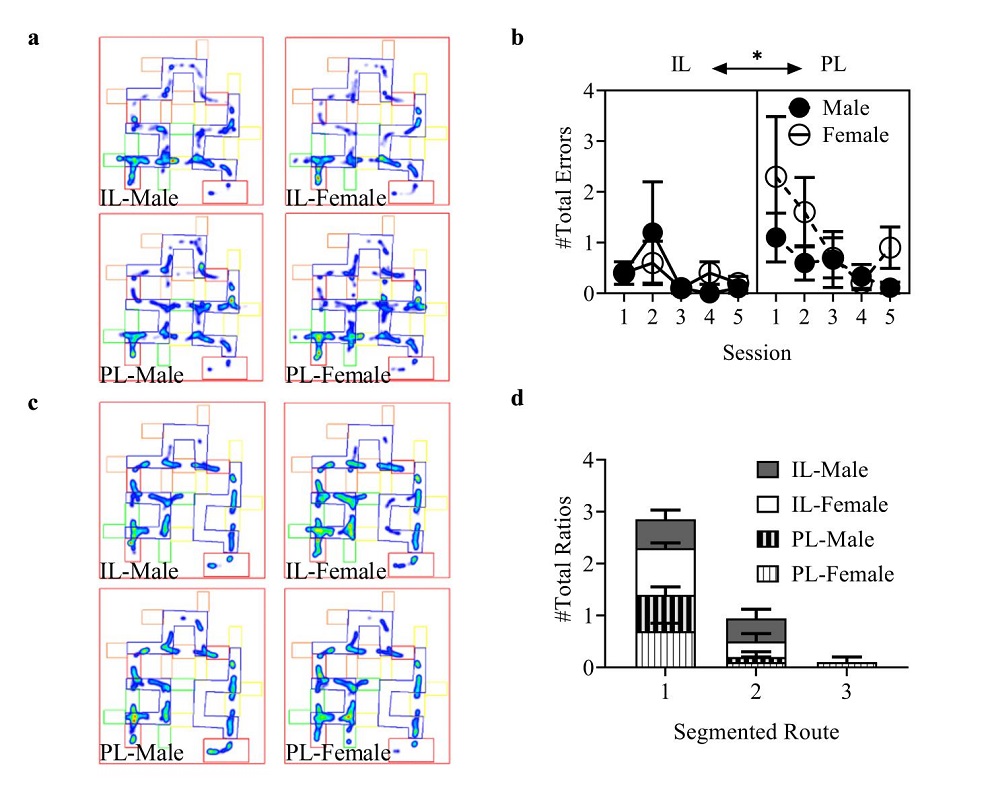
Figure 4. Comparisons of segmented routes during the generalization/analysis task and the segment fixation task. Note. a) Heat map comparison of group behavior during the first session of the generalization/analysis task. b) Comparison of the number of total errors during the five sessions of the generalization/analysis task. c) Heat map comparison of group behavior during the last session of the segment fixation task. d) Comparisons of total ratios of fixation to different segmented routes among groups during the four sessions of the segment fixation task. Note that the higher the brightness of the heat map, the higher the exploration density. The position of the circle symbol or the height of the column in the chart represents the average value or the percentage of each group in each trial/session, and the error bar represents the standard error. *p< 0.05.
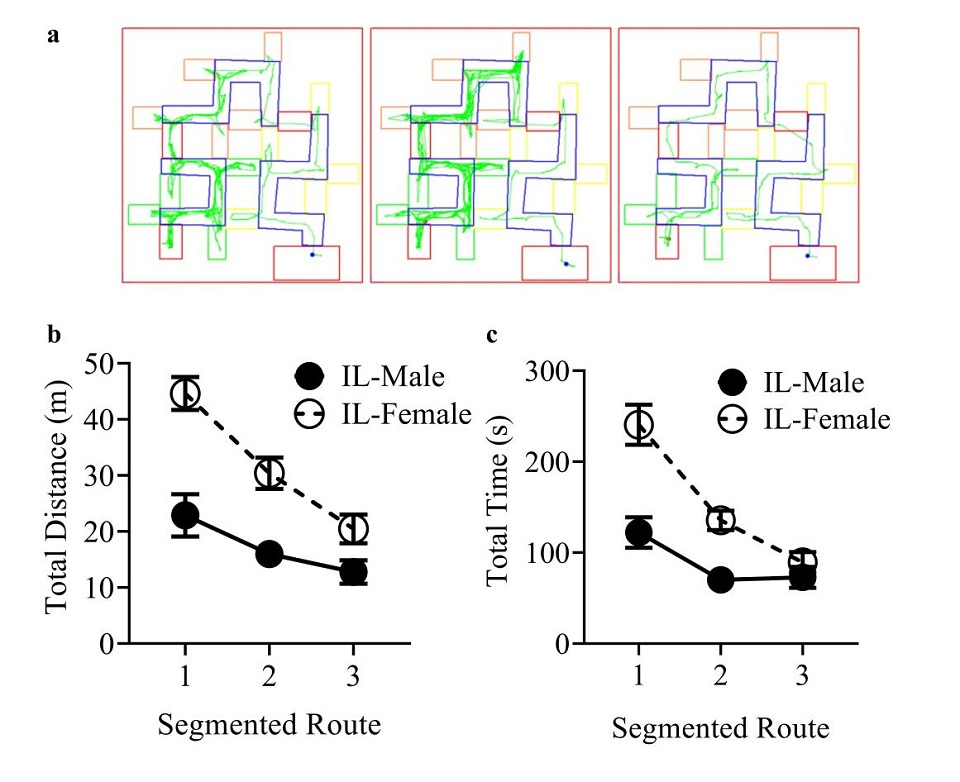
Figure 5. Results of segmented route analysis of the IL group during the learning stage. Note. a) Typical trajectory of the IL group, showing IL-Female-2-1, IL-Female-6-1 and IL-Female-9-1, respectively (from left to right). Panels b) and c) represent the IL group’s travel distance and travel time, respectively. The travel time of the segmented route is calculated as that “the traveling time = the duration of traveling time - the duration of staying static at the starting area”, so as to eliminate the systematic error caused by the fixation to the starting area when calculating the traveling time of the first segmented route. In terms of total distance or total time, the three data points of “1st segmented route”, “2nd segmented route” and “3rd segmented route” of each IL rat were the sum of distance or time traveled across days before “learning success” happened. “Learning success” was defined as when a rat can reliably achieve zero errors reaching the end of the maze - the food box, and it is different from individual to individual. Only the travel distance or time in the range of days before “learning success” happened were analyzed because we aimed to focus on the learning process “from zero to one”, without being affected by the subjects’ behavioral performance after the “learning success”. The position of the circle symbol in the chart shows the average value of each group in each trial, and the error bar shows the standard error.

Figure 6. Heat maps showing exploration density after opening a new segment during learning in the PL group. Note. The heat map shows the 4th session and the 8th session of the PL group in the learning stage. The higher the color brightness, the higher the density of exploring the area.
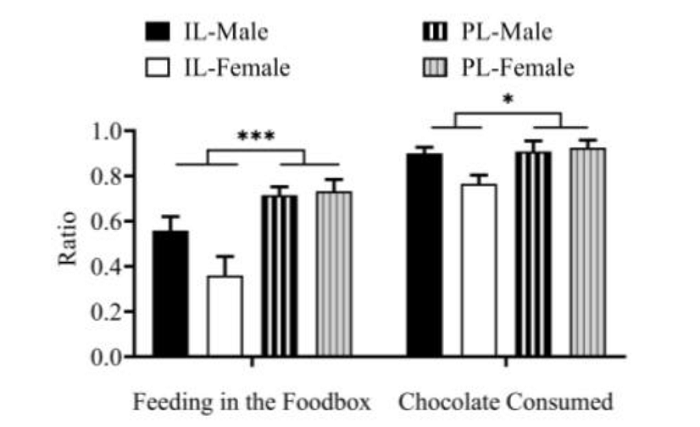
Figure 7. Between-group comparisons of feeding behavior at the endpoint of the maze. Note. The ratio refers to the number of sessions in which the subjects fed in the food box or consumed chocolate pellets when reaching the endpoint of the maze as a percentage of the total number of sessions during the learning stage. The height of the column in the figure shows the mean value, and the error bar shows the standard error. *p < 0.05, *** p < 0.001.
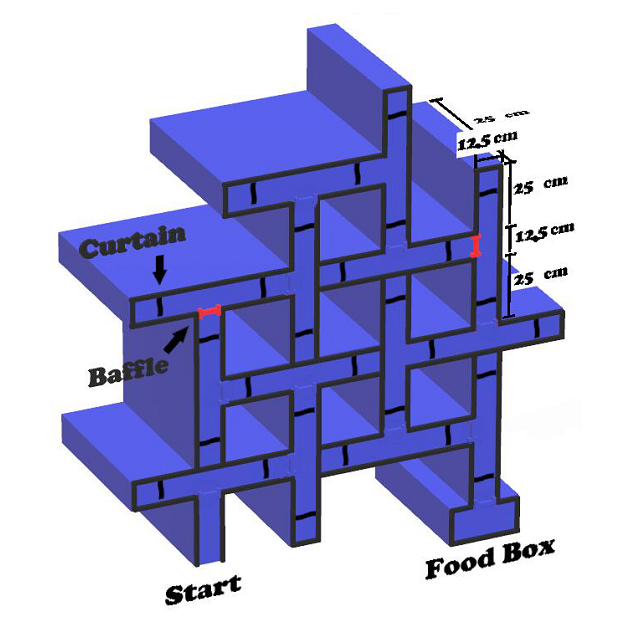
Figure S1. Design of the 14-unit composite T-maze. Note. It includes the curtains, the partition boards and the food box (on the left end of the food box there was a rectangular black porcelain bowl). The maze is used throughout the whole study.
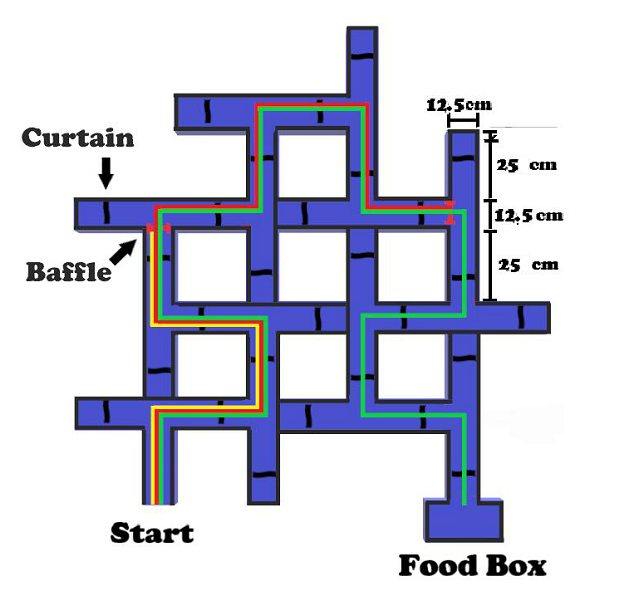
Figure S2. Design of the learning task and the one-week-later retest task. Note. The retractable (black) baffle marked in red was only for the learning stage of the PL group. The baffle was placed in a slot and can be inserted. The yellow route, the red route and the green route were the correct routes for the PL group for Session 1 ~ 3, Session 4 ~ 7 and Session 8 ~ 12, respectively, and the green route was the correct route for the IL group as well. During the retest task stage, all routes were open for both the IL and the PL groups.
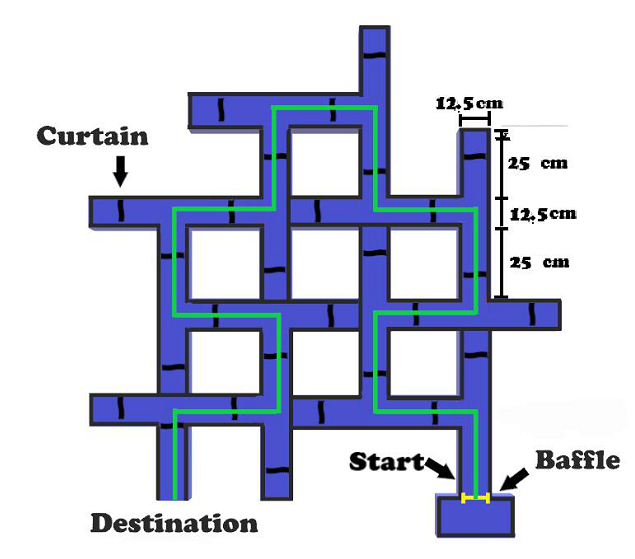
Figure S3. Design of the Gestalt transfer learning task. Note. The “food box” entrance was sealed by a clapboard marked in yellow and then changed to the “starting point”. The curtain of the original starting point was moved to the new starting point.
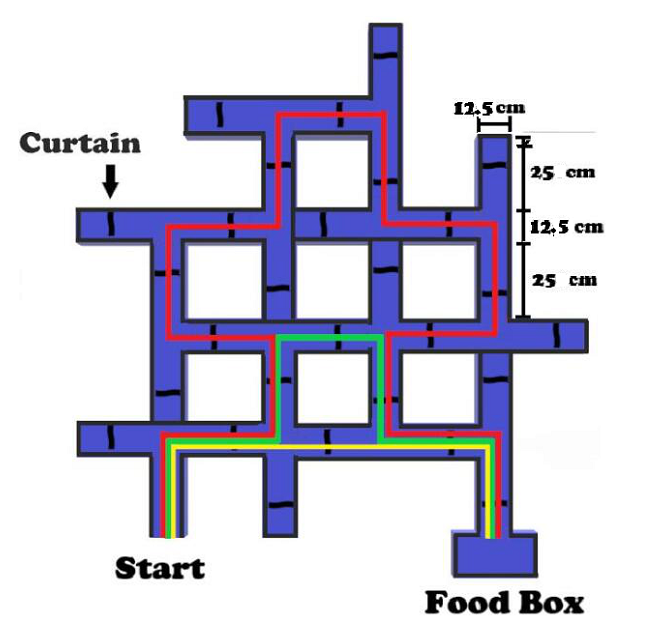
Figure S4. Design of the generalization/analysis task. Note. Yellow, red and green routes were the shortest route, the original route and the hidden route, respectively. The hidden route was named because the partition board behind a curtain in the originally wrong area was removed, allowing the subject to get through.
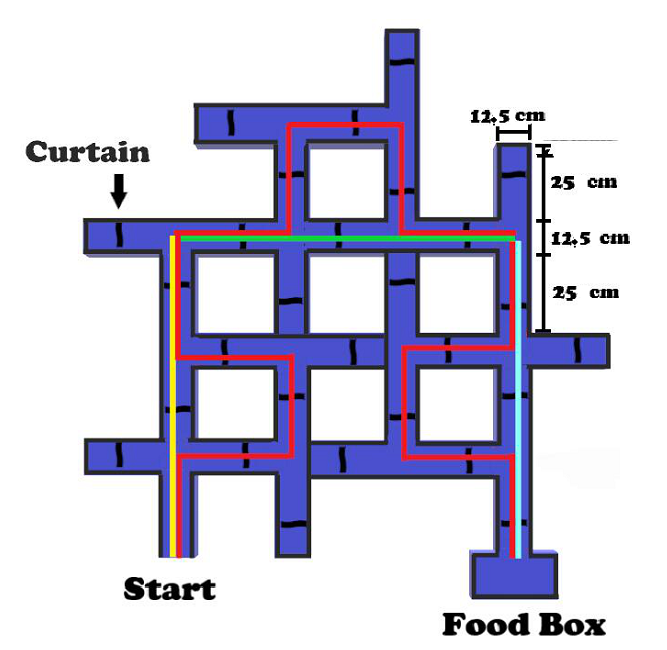
Figure S5. Design of the segment fixation task. Note. Yellow, green and blue routes were the shortest routes in the first, the second and the third segments, respectively.
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 3090.72 | 11 | 280.00 | F (11, 396) = 29.42*** | 0.000 | 0.45 |
| Learning mode | 141.92 | 1 | 141.92 | F (1, 36) = 15.54*** | 0.000 | 0.30 |
| Sex | 105.47 | 1 | 105.47 | F (1, 36) = 11.55** | 0.002 | 0.24 |
| Session × Learning mode | 2940.81 | 11 | 267.35 | F (11, 396) = 27.99*** | 0.000 | 0.44 |
| Session × Sex | 257.46 | 11 | 23.41 | F (11, 396) = 2.45** | 0.006 | 0.06 |
| Learning mode × Sex | 79.22 | 1 | 79.22 | F(1, 36) = 8.67** | 0.006 | 0.19 |
| Session × Learning mode × Sex | 191 | 11 | 17.36 | F (11, 396) = 1.82* | 0.048 | 0.05 |
Table S1. Results of a three-factor repeated measures analysis of variance of the number of errors in the learning stage
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 3090.72 | 11 | 280.00 | F (11, 396) = 29.42*** | 0.000 | 0.45 |
| Learning mode | 141.92 | 1 | 141.92 | F (1, 36) = 15.54*** | 0.000 | 0.30 |
| Sex | 105.47 | 1 | 105.47 | F (1, 36) = 11.55** | 0.002 | 0.24 |
| Session × Learning mode | 2940.81 | 11 | 267.35 | F (11, 396) = 27.99*** | 0.000 | 0.44 |
| Session × Sex | 257.46 | 11 | 23.41 | F (11, 396) = 2.45** | 0.006 | 0.06 |
| Learning mode × Sex | 79.22 | 1 | 79.22 | F(1, 36) = 8.67** | 0.006 | 0.19 |
| Session × Learning mode × Sex | 191 | 11 | 17.36 | F (11, 396) = 1.82* | 0.048 | 0.05 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Sex | 13.23 | 1 | 13.23 | F(1, 36) = 0.73 | 0.551 | 0.42 |
| Learning mode | 60.03 | 1 | 60.03 | F (1, 36) = 3.29 | 0.321 | 0.77 |
| Sex × Learning mode | 18.23 | 1 | 18.23 | F (1, 36) = 3.45 | 0.072 | 0.09 |
Table S2. Results of a two-factor complete random analysis of variance on the number of days to learning success
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Sex | 13.23 | 1 | 13.23 | F(1, 36) = 0.73 | 0.551 | 0.42 |
| Learning mode | 60.03 | 1 | 60.03 | F (1, 36) = 3.29 | 0.321 | 0.77 |
| Sex × Learning mode | 18.23 | 1 | 18.23 | F (1, 36) = 3.45 | 0.072 | 0.09 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Sex | 13.23 | 1 | 13.23 | F(1, 36) = 2.50 | 0.122 | 0.07 |
| Learning mode | 60.03 | 1 | 60.03 | F (1, 36) = 11.36** | 0.002 | 0.24 |
Table S3. Results of post-hoc multiple comparisons of the number of days to learning success
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Sex | 13.23 | 1 | 13.23 | F(1, 36) = 2.50 | 0.122 | 0.07 |
| Learning mode | 60.03 | 1 | 60.03 | F (1, 36) = 11.36** | 0.002 | 0.24 |
| t | p | Cohen’s d | |
|---|---|---|---|
| Male | 4.12*** | 0.000 | -1.84 |
| Female | 0.98 | 0.341 | -0.44 |
Table S4. A comparison of the simple effects of learning modes at the sex level
| t | p | Cohen’s d | |
|---|---|---|---|
| Male | 4.12*** | 0.000 | -1.84 |
| Female | 0.98 | 0.341 | -0.44 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 3.82 | 2 | 1.91 | F (2, 72) = 2.19 | 0.120 | 0.06 |
| Learning style | 10.21 | 1 | 10.21 | F(1, 36) = 4.03 | 0.052 | 0.10 |
| Sex | 3.01 | 1 | 3.01 | F(1, 36) = 1.19 | 0.283 | 0.03 |
| Session×Learning style | 3.02 | 2 | 1.51 | F(2, 72) = 1.73 | 0.185 | 0.05 |
| Session×Sex | 0.52 | 2 | 0.26 | F(2, 72) = 0.30 | 0.745 | 0.01 |
| Learning Style×Sex | 0.01 | 1 | 0.01 | F (1, 36) = 0.00 | 0.955 | 0.00 |
| Session×Learning style×Sex | 0.52 | 2 | 0.26 | F (2, 72) = 0.30 | 0.745 | 0.01 |
Table S5. Results of a three-factor repeated measures analysis of variance of the retest stage after one week of learning
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 3.82 | 2 | 1.91 | F (2, 72) = 2.19 | 0.120 | 0.06 |
| Learning style | 10.21 | 1 | 10.21 | F(1, 36) = 4.03 | 0.052 | 0.10 |
| Sex | 3.01 | 1 | 3.01 | F(1, 36) = 1.19 | 0.283 | 0.03 |
| Session×Learning style | 3.02 | 2 | 1.51 | F(2, 72) = 1.73 | 0.185 | 0.05 |
| Session×Sex | 0.52 | 2 | 0.26 | F(2, 72) = 0.30 | 0.745 | 0.01 |
| Learning Style×Sex | 0.01 | 1 | 0.01 | F (1, 36) = 0.00 | 0.955 | 0.00 |
| Session×Learning style×Sex | 0.52 | 2 | 0.26 | F (2, 72) = 0.30 | 0.745 | 0.01 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 1071.55 | 2 | 535.28 | F (2, 72) = 25.64*** | 0.000 | 0.42 |
| Learning mode | 130.21 | 1 | 130.21 | F (1, 36) = 5.50* | 0.025 | 0.13 |
| Sex | 118.01 | 1 | 118.01 | F (1, 36) = 4.99* | 0.032 | 0.12 |
| Session × Learning mode | 1.72 | 2 | 0.86 | F (2, 72) = 0.04 | 0.960 | 0.00 |
| Session × Sex | 21.72 | 2 | 10.86 | F (2, 72) = 0.52 | 0.597 | 0.01 |
| Learning mode × Sex | 2.41 | 1 | 2.41 | F (1, 36) = 0.10 | 0.752 | 0.00 |
| Session × Learning mode × Sex | 5.02 | 2 | 2.51 | F (2, 72) = 0.12 | 0.887 | 0.00 |
Table S6. Results of a three-factor repeated measures analysis of variance of the number of errors in the Gestalt transfer learning stage
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 1071.55 | 2 | 535.28 | F (2, 72) = 25.64*** | 0.000 | 0.42 |
| Learning mode | 130.21 | 1 | 130.21 | F (1, 36) = 5.50* | 0.025 | 0.13 |
| Sex | 118.01 | 1 | 118.01 | F (1, 36) = 4.99* | 0.032 | 0.12 |
| Session × Learning mode | 1.72 | 2 | 0.86 | F (2, 72) = 0.04 | 0.960 | 0.00 |
| Session × Sex | 21.72 | 2 | 10.86 | F (2, 72) = 0.52 | 0.597 | 0.01 |
| Learning mode × Sex | 2.41 | 1 | 2.41 | F (1, 36) = 0.10 | 0.752 | 0.00 |
| Session × Learning mode × Sex | 5.02 | 2 | 2.51 | F (2, 72) = 0.12 | 0.887 | 0.00 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 24.54 | 4 | 6.13 | F(4, 140) = 3.00* | 0.020 | 0.08 |
| Learning mode | 12.60 | 1 | 12.60 | F(1, 35) = 4.66* | 0.038 | 0.12 |
| Sex | 3.58 | 1 | 3.58 | F(1, 35) = 1.32 | 0.258 | 0.04 |
| Session × Learning mode | 9.10 | 4 | 2.28 | F(4, 140) = 1.11 | 0.352 | 0.03 |
| Session × Sex | 2.23 | 4 | 0.56 | F(4, 140) = 0.27 | 0.895 | 0.01 |
| Learning mode × Sex | 4.12 | 1 | 4.12 | F(1, 35) = 1.53 | 0.225 | 0.04 |
| Session × Learning mode × Sex | 6.88 | 4 | 1.72 | F(4, 140) = 0.84 | 0.500 | 0.02 |
Table S7. Results of a three-factor repeated measures analysis of variance for the five-day Generalization test stage
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Session | 24.54 | 4 | 6.13 | F(4, 140) = 3.00* | 0.020 | 0.08 |
| Learning mode | 12.60 | 1 | 12.60 | F(1, 35) = 4.66* | 0.038 | 0.12 |
| Sex | 3.58 | 1 | 3.58 | F(1, 35) = 1.32 | 0.258 | 0.04 |
| Session × Learning mode | 9.10 | 4 | 2.28 | F(4, 140) = 1.11 | 0.352 | 0.03 |
| Session × Sex | 2.23 | 4 | 0.56 | F(4, 140) = 0.27 | 0.895 | 0.01 |
| Learning mode × Sex | 4.12 | 1 | 4.12 | F(1, 35) = 1.53 | 0.225 | 0.04 |
| Session × Learning mode × Sex | 6.88 | 4 | 1.72 | F(4, 140) = 0.84 | 0.500 | 0.02 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 9.70 | 2 | 4.85 | F (2, 70) = 40.83*** | 0.000 | 0.54 |
| Learning mode | 0.20 | 1 | 0.20 | F (1, 35) = 1.18 | 0.286 | 0.03 |
| Sex | 0.07 | 1 | 0.07 | F (1, 35) = 0.42 | 0.520 | 0.01 |
| Learning mode × Sex | 0.01 | 1 | 0.01 | F (1, 35) = 0.05 | 0.830 | 0.00 |
| Order of segment × Learning mode | 0.55 | 2 | 0.28 | F (2, 70) = 2.32 | 0.106 | 0.06 |
| Order of segment × Sex | 0.29 | 2 | 0.15 | F (2, 70) = 1.22 | 0.300 | 0.03 |
| Order of Segment × Learning mode × Sex | 0.36 | 2 | 0.18 | F (2, 70) = 1.50 | 0.231 | 0.04 |
Table S8. Results of a three-factor repeated measures analysis of variance for the proportion of rats remaining choosing the original route during the final session of the segment fixation test stage
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 9.70 | 2 | 4.85 | F (2, 70) = 40.83*** | 0.000 | 0.54 |
| Learning mode | 0.20 | 1 | 0.20 | F (1, 35) = 1.18 | 0.286 | 0.03 |
| Sex | 0.07 | 1 | 0.07 | F (1, 35) = 0.42 | 0.520 | 0.01 |
| Learning mode × Sex | 0.01 | 1 | 0.01 | F (1, 35) = 0.05 | 0.830 | 0.00 |
| Order of segment × Learning mode | 0.55 | 2 | 0.28 | F (2, 70) = 2.32 | 0.106 | 0.06 |
| Order of segment × Sex | 0.29 | 2 | 0.15 | F (2, 70) = 1.22 | 0.300 | 0.03 |
| Order of Segment × Learning mode × Sex | 0.36 | 2 | 0.18 | F (2, 70) = 1.50 | 0.231 | 0.04 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Segmented route | 2987.87 | 2 | 1493.94 | F (2, 36) = 38.01*** | 0.000 | 0.68 |
| Sex | 3208.63 | 1 | 3208.63 | F (1, 18) = 22.51*** | 0.000 | 0.56 |
| Segmented route×Sex | 492.36 | 2 | 246.18 | F(2, 36) = 6.26** | 0.005 | 0.26 |
Table S9. Results of a two-factor repeated measures analysis of variance for the travel distances of different segmented routes in the IL group
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Segmented route | 2987.87 | 2 | 1493.94 | F (2, 36) = 38.01*** | 0.000 | 0.68 |
| Sex | 3208.63 | 1 | 3208.63 | F (1, 18) = 22.51*** | 0.000 | 0.56 |
| Segmented route×Sex | 492.36 | 2 | 246.18 | F(2, 36) = 6.26** | 0.005 | 0.26 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Segmented route | 111308.10 | 2 | 55654.05 | F (2, 36) = 39.10*** | 0.000 | 0.69 |
| Sex | 67002.42 | 1 | 67002.42 | F(1, 18) = 22.10*** | 0.000 | 0.55 |
| Segmented route×Sex | 25910.57 | 2 | 12955.29 | F (2, 36) = 9.10** | 0.001 | 0.34 |
Table S10. Results of a two-factor repeated measures analysis of variance for the travel time of different segmented routes in the IL group
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Segmented route | 111308.10 | 2 | 55654.05 | F (2, 36) = 39.10*** | 0.000 | 0.69 |
| Sex | 67002.42 | 1 | 67002.42 | F(1, 18) = 22.10*** | 0.000 | 0.55 |
| Segmented route×Sex | 25910.57 | 2 | 12955.29 | F (2, 36) = 9.10** | 0.001 | 0.34 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 2.99 | 1 | 2.09 | F(1, 18) = 0.70 | 0.412 | 0.04 |
| Session | 191.85 | 3 | 63.95 | F(3, 54) = 7.07*** | 0.000 | 0.28 |
| Sex | 0.00 | 1 | 0.00 | F(1, 18) = 0.00 | 0.995 | 0.00 |
| Order of segment × Sex | 22.68 | 1 | 22.68 | F(1, 18) = 5.35* | 0.033 | 0.23 |
| Session × Sex | 59.15 | 3 | 19.72 | F(3, 54) = 2.18 | 0.101 | 0.11 |
| Order of segment × Session | 23.39 | 3 | 7.80 | F(3, 54) = 2.00 | 0.124 | 0.10 |
| Order of segment × Session × Sex | 36.50 | 3 | 12.17 | F(3, 54) = 3.13* | 0.033 | 0.15 |
Table S11. Results of a three-factor repeated measures analysis of variance for the travel distances of the 2nd segmented route in the PL group
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 2.99 | 1 | 2.09 | F(1, 18) = 0.70 | 0.412 | 0.04 |
| Session | 191.85 | 3 | 63.95 | F(3, 54) = 7.07*** | 0.000 | 0.28 |
| Sex | 0.00 | 1 | 0.00 | F(1, 18) = 0.00 | 0.995 | 0.00 |
| Order of segment × Sex | 22.68 | 1 | 22.68 | F(1, 18) = 5.35* | 0.033 | 0.23 |
| Session × Sex | 59.15 | 3 | 19.72 | F(3, 54) = 2.18 | 0.101 | 0.11 |
| Order of segment × Session | 23.39 | 3 | 7.80 | F(3, 54) = 2.00 | 0.124 | 0.10 |
| Order of segment × Session × Sex | 36.50 | 3 | 12.17 | F(3, 54) = 3.13* | 0.033 | 0.15 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 137.60 | 1 | 137.60 | F(1, 18) = 0.13 | 0.722 | 0.01 |
| Session | 34073.62 | 3 | 11357.87 | F(3, 54) = 8.00*** | 0.000 | 0.31 |
| Sex | 549.60 | 1 | 549.60 | F(1, 18) = 0.30 | 0.589 | 0.02 |
| Order of segment × Sex | 4361.62 | 1 | 4361.62 | F(1, 18) = 4.14 | 0.057 | 0.19 |
| Session × Sex | 3598.01 | 3 | 1199.34 | F(3, 54) = 0.85 | 0.475 | 0.05 |
| Order of segment × Session | 2163.39 | 3 | 721.13 | F(3, 54) = 0.81 | 0.496 | 0.04 |
| Order of segment × Session × Sex | 2471.07 | 3 | 823.69 | F(3, 54) = 0.92 | 0.437 | 0.05 |
Table S12. Results of a three-factor repeated measures analysis of variance for the travel time of the 2nd segmented route in the PL group
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 137.60 | 1 | 137.60 | F(1, 18) = 0.13 | 0.722 | 0.01 |
| Session | 34073.62 | 3 | 11357.87 | F(3, 54) = 8.00*** | 0.000 | 0.31 |
| Sex | 549.60 | 1 | 549.60 | F(1, 18) = 0.30 | 0.589 | 0.02 |
| Order of segment × Sex | 4361.62 | 1 | 4361.62 | F(1, 18) = 4.14 | 0.057 | 0.19 |
| Session × Sex | 3598.01 | 3 | 1199.34 | F(3, 54) = 0.85 | 0.475 | 0.05 |
| Order of segment × Session | 2163.39 | 3 | 721.13 | F(3, 54) = 0.81 | 0.496 | 0.04 |
| Order of segment × Session × Sex | 2471.07 | 3 | 823.69 | F(3, 54) = 0.92 | 0.437 | 0.05 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 29.19 | 2 | 14.60 | F(2, 36) = 15.86*** | 0.000 | 0.47 |
| Session | 48.08 | 4 | 12.02 | F(4, 72) = 5.53** | 0.001 | 0.24 |
| Sex | 0.69 | 1 | 0.69 | F(1, 18) = 0.43 | 0.523 | 0.02 |
| Order of segment × Sex | 4.74 | 2 | 2.37 | F(2, 36) = 2.57 | 0.090 | 0.13 |
| Session × Sex | 5.53 | 4 | 1.38 | F(4, 72) = 0.64 | 0.638 | 0.03 |
| Order of segment × Session | 15.85 | 8 | 1.98 | F(8, 144) = 2.33* | 0.022 | 0.11 |
| Order of Segment × Session × Sex | 2.10 | 8 | 0.26 | F(8, 144) = 0.31 | 0.962 | 0.02 |
Table S13. Results of a three-factor repeated measures analysis of variance for the travel distances of the 3rd segmented route in the PL group
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 29.19 | 2 | 14.60 | F(2, 36) = 15.86*** | 0.000 | 0.47 |
| Session | 48.08 | 4 | 12.02 | F(4, 72) = 5.53** | 0.001 | 0.24 |
| Sex | 0.69 | 1 | 0.69 | F(1, 18) = 0.43 | 0.523 | 0.02 |
| Order of segment × Sex | 4.74 | 2 | 2.37 | F(2, 36) = 2.57 | 0.090 | 0.13 |
| Session × Sex | 5.53 | 4 | 1.38 | F(4, 72) = 0.64 | 0.638 | 0.03 |
| Order of segment × Session | 15.85 | 8 | 1.98 | F(8, 144) = 2.33* | 0.022 | 0.11 |
| Order of Segment × Session × Sex | 2.10 | 8 | 0.26 | F(8, 144) = 0.31 | 0.962 | 0.02 |
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 2253.81 | 2 | 1126.90 | F(2, 36) = 30.87*** | 0.000 | 0.63 |
| Session | 3101.67 | 4 | 775.42 | F(4, 72) = 12.86*** | 0.000 | 0.42 |
| Sex | 28.92 | 1 | 28.92 | F(1, 18) = 0.46 | 0.506 | 0.03 |
| Order of segment × Sex | 176.73 | 2 | 88.37 | F(2, 36) = 2.42 | 0.103 | 0.12 |
| Session × Sex | 98.90 | 4 | 24.72 | F(4, 72) = 0.41 | 0.801 | 0.02 |
| Order of segment × Session | 2023.60 | 8 | 252.95 | F(8, 144) = 10.84*** | 0.000 | 0.38 |
| Order of Segment × Session × Sex | 214.13 | 8 | 26.77 | F(8, 144) = 1.15 | 0.335 | 0.06 |
Table S14. Results of a three-factor repeated measures analysis of variance for the travel time of the 3rd segmented route in the PL group
| SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|
| Order of segment | 2253.81 | 2 | 1126.90 | F(2, 36) = 30.87*** | 0.000 | 0.63 |
| Session | 3101.67 | 4 | 775.42 | F(4, 72) = 12.86*** | 0.000 | 0.42 |
| Sex | 28.92 | 1 | 28.92 | F(1, 18) = 0.46 | 0.506 | 0.03 |
| Order of segment × Sex | 176.73 | 2 | 88.37 | F(2, 36) = 2.42 | 0.103 | 0.12 |
| Session × Sex | 98.90 | 4 | 24.72 | F(4, 72) = 0.41 | 0.801 | 0.02 |
| Order of segment × Session | 2023.60 | 8 | 252.95 | F(8, 144) = 10.84*** | 0.000 | 0.38 |
| Order of Segment × Session × Sex | 214.13 | 8 | 26.77 | F(8, 144) = 1.15 | 0.335 | 0.06 |
| SS | SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|---|
| Weight | Learning mode | 2793.68 | 1 | 2793.68 | F (1, 36) = 2.80 | 0.103 | 0.07 |
| Sex | 44.41 | 1 | 44.41 | F (1, 36) = 0.04 | 0.834 | 0.00 | |
| Learning mode × Sex | 1387.20 | 1 | 1387.20 | F (1, 36) = 1.39 | 0.246 | 0.37 | |
| Resting time in the start area | Learning mode | 7.31 | 1 | 7.31 | F (1, 36) = 0.64 | 0.429 | 0.02 |
| Sex | 25.60 | 1 | 25.60 | F (1, 36) = 2.24 | 0.143 | 0.06 | |
| Learning mode × Sex | 28.10 | 1 | 28.10 | F(1, 36) = 2.46 | 0.126 | 0.06 | |
| Feeding in the food box | Learning mode | 8.01 | 1 | 8.01 | F (1, 34) = 15.93*** | 0.000 | 0.32 |
| Sex | 0.78 | 1 | 0.78 | F (1, 34) = 1.55 | 0.222 | 0.04 | |
| Learning mode × Sex | 1.47 | 1 | 1.47 | F (1, 34) = 2.92 | 0.097 | 0.08 | |
| Chocolate Consumed | Learning mode | 0.83 | 1 | 0.83 | F (1, 36) = 5.07* | 0.031 | 0.12 |
| Sex | 0.41 | 1 | 0.41 | F (1, 36) = 2.49 | 0.124 | 0.07 | |
| Learning mode × Sex | 0.68 | 1 | 0.68 | F (1, 36) = 4.11 | 0.050 | 0.10 |
Table S15. Between-subjects results of a three-factor repeated measures analysis of variance on learning mode adaptability in the learning stage
| SS | SS | df | MS | F (dfn, dfd) | p | η2 | |
|---|---|---|---|---|---|---|---|
| Weight | Learning mode | 2793.68 | 1 | 2793.68 | F (1, 36) = 2.80 | 0.103 | 0.07 |
| Sex | 44.41 | 1 | 44.41 | F (1, 36) = 0.04 | 0.834 | 0.00 | |
| Learning mode × Sex | 1387.20 | 1 | 1387.20 | F (1, 36) = 1.39 | 0.246 | 0.37 | |
| Resting time in the start area | Learning mode | 7.31 | 1 | 7.31 | F (1, 36) = 0.64 | 0.429 | 0.02 |
| Sex | 25.60 | 1 | 25.60 | F (1, 36) = 2.24 | 0.143 | 0.06 | |
| Learning mode × Sex | 28.10 | 1 | 28.10 | F(1, 36) = 2.46 | 0.126 | 0.06 | |
| Feeding in the food box | Learning mode | 8.01 | 1 | 8.01 | F (1, 34) = 15.93*** | 0.000 | 0.32 |
| Sex | 0.78 | 1 | 0.78 | F (1, 34) = 1.55 | 0.222 | 0.04 | |
| Learning mode × Sex | 1.47 | 1 | 1.47 | F (1, 34) = 2.92 | 0.097 | 0.08 | |
| Chocolate Consumed | Learning mode | 0.83 | 1 | 0.83 | F (1, 36) = 5.07* | 0.031 | 0.12 |
| Sex | 0.41 | 1 | 0.41 | F (1, 36) = 2.49 | 0.124 | 0.07 | |
| Learning mode × Sex | 0.68 | 1 | 0.68 | F (1, 36) = 4.11 | 0.050 | 0.10 |

Note. The correct route of the maze was divided into three segments with shape similarity, i.e. the first segmented route, the second segmented route and the third segmented route, labeled red, green and yellow, respectively.

Note. The baffle marked in red was only for the learning stage of the PL group. The yellow, red and green routes are the correct routes for Session 1-3, Session 4-7 and Session 8-12, respectively.
Note. In the generalization/analysis task, the routes marked in yellow, red and green are the shortest route, the original route and the hidden route (with the partition behind the curtain removed in the wrong route area), respectively.
Note. In the segment fixation task, the routes marked in yellow, green and sky-blue are the shortest routes of the first, second and third segments respectively. The original route (marked in red) remains unblocked.
| [1] |
Bannerman, D. M., Good, M. A., Butcher, S. P., Ramsay, M., & Morris, R. G. M. (1995). Distinct components of spatial learning revealed by prior training and NMDA receptor blockade. Nature, 378(6553), 182-186.
doi: 10.1038/378182a0 URL pmid: 7477320 |
| [2] |
Bechtholt, A. J., Hill, T. E., & Lucki, I. (2007). Anxiolytic effect of serotonin depletion in the novelty-induced hypophagia test. Psychopharmacology, 190(4), 531-540.
doi: 10.1007/s00213-006-0615-9 URL |
| [3] | Chen, Q., Chen, Q., & Zhang, J. W. (2003). A model of Integrative Learning in the information era. Peking University Education Review, (3), 90-96. |
| [4] |
Dulawa, Dulawa, S. C., & Hen, R. (2005). Recent advances in animal models of chronic antidepressant effects: The novelty-induced hypophagia test. Neuroscience & Biobehavioral Reviews, 29(4-5), 771-783.
doi: 10.1016/j.neubiorev.2005.03.017 URL pmid: 15890403 |
| [5] | Dulawa, Dulawa, S. C. (2009). Novelty-induced hypophagia. Neuromethods, 42, 247-259. |
| [6] |
Dusek, Dusek, J. A., & Eichenbaum, H. (1997). The hippocampus and memory for orderly stimulus relations. Proceedings of the National Academy of Sciences of the United States of America, 94(13), 7109-7114.
doi: 10.1073/pnas.94.13.7109 URL pmid: 9192700 |
| [7] | , Fang, H. L. (2018). Integrative learning in general education curriculum: The case of a great book reading course. Fudan Education Forum, 16(2), 61+67+62-66. |
| [8] |
Hawley, W. R., Grissom, E. M., Barratt, H. E., Conrad, T. S., & Dohanich, G. P. (2012). The effects of biological sex and gonadal hormones on learning strategy in adult rats. Physiology & Behavior, 105(4), 1014-1020.
doi: 10.1016/j.physbeh.2011.11.021 URL pmid: 22146478 |
| [9] |
Keeley, R. J., Tyndall, A. V., Scott, G. A., & Saucier, D. M. (2013). Sex difference in cue strategy in a modified version of the Morris water task: Correlations between brain and behaviour. PLoS One, 8, e69727.
URL pmid: 23874990 |
| [10] | Lian, R. (2019). Effects of different learning styles on vocabulary memory. Master's thesis of Fujian Normal University, (Li, Q.), 7. |
| [11] | Liu, R. (2002). On conception of learning of college students. Journal of Higher Education, (4), 77-81. |
| [12] | Marshall, H. H. (1992). Redefining student learning: Roots of educational change. Ablex Pub. Corp. |
| [13] |
Munion, A. K., Stefanucci, J. K., Rovira, E., Squire, P., & Hendricks, M. (2019). Gender differences in spatial navigation: Characterizing wayfinding behaviors. Psychonomic Bulletin & Review, 26(6), 1933-1940.
doi: 10.3758/s13423-019-01659-w URL pmid: 31432331 |
| [14] |
Perrot-Sinal, T. S., Kostenuik, M. A., Ossenkopp, K. P., & Kavaliers, M. (1996). Sex differences in performance in the Morris water maze and the effects of initial nonstationary hidden platform training. Behavioral Neuroscience, 110(6), 1309-1320.
doi: 10.1037//0735-7044.110.6.1309 URL pmid: 8986334 |
| [15] |
Roof R. L. (1993). Neonatal exogenous testosterone modifies sex difference in radial arm and Morris water maze performance in prepubescent and adult rats. Behavioural Brain Research, 53(1-2), 1-10.
URL pmid: 8466654 |
| [16] |
Saucier, D & Cain, D. P. (1995). Spatial learning without NMDA receptor-dependent long-term potentiation. Nature, 378(6553), 186-189.
URL pmid: 7477321 |
| [17] |
Saucier, D. M., Shultz, S. R., Keller, A. J., Cook, C. M., & Binsted, G. (2008). Sex differences in object location memory and spatial navigation in Long-Evans rats. Animal Cognition, 11(1), 129-137.
doi: 10.1007/s10071-007-0096-1 URL pmid: 17562087 |
| [18] | Schraw, G. (1998). Promoting general metacognitive awareness. Instructional Science, 26(1/2), 113-125. |
| [19] | Shi, L. F.(2000). Learning theory: The principle and theory of learning psychology. Beijing, China: People’s Educational Press. |
| [20] | Skinner B. F. (1945). The operational analysis of psychological terms. Psychological Review, 52(4), 547-553. |
| [21] |
Sneider, J. T., Hamilton, D. A., Cohen-Gilbert, J. E., Crowley, D. J., Rosso, I. M., & Silveri, M. M. (2015). Sex differences in spatial navigation and perception in human adolescents and emerging adults. Behavioural Processes, 111, 42-50.
URL pmid: 25464337 |
| [22] |
Tolman E. C. (1948). Cognitive maps in rats and men. Psychological Review, 55(4), 189-208.
URL pmid: 18870876 |
| [23] |
Walton, Walton G. M., & Yeager, D. S. (2020) Seed and soil: Psychological affordances in contexts help to explain where wise interventions succeed or fail. Current Directions in Psychological Science, 29(3), 219-226.
URL pmid: 32719574 |
| [24] | Wang, Y., & Su, Y. J. (2001). Mazes and animal behavioral research. Advances in Psychological Science,(3), 264-269. |
| [25] |
Yeager, D. S., & Walton, G. M. (2011). Social-psychological interventions in education: they’re not magic. Review of Educational Research, 81(2), 267-301.
doi: 10.3102/0034654311405999 URL |
| [26] | Zhang, H. (2003). Behaviorist Psychology. Hangzhou, China: Zhejiang Educational Press. |
| [27] | Zhou Z. H. (2005a). On the common characters between E. L. Thorndike and B. F. Skinner in learning theory. Journal of Shaoyang University (Social Science), 4(6), 157-159. |
| [28] | Zhou, Z. H. (2005b). The difference in learning theory between Thorndike and Skinner. Journal of Hunan First Normal College, 5(3), 34-37. |
| [29] | Zhu, Y. (2019). Ethics in psychological research. Psychological Exploration, 39(02), 99-108. |
| [30] | Zhu, Y., He, W., & Wang, Y. F. (2017). Challenge-hindrance stress and academic achievement: Proactive personality as moderator. Social Behavior and Personality, 45(3), 441-452. |
| [1] | Guan Linchu,Cui Qiugeng Institute of Psychology, Academia Sinica. INVESTIGATION INTO ANIMAL MODELS OF LEARNING AND MEMORY DISORDER INDUCED BY ANISODINE [J]. , 1992, 24(01): 75-81. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||